為了幫助廣大考生復習好、考好數學,下面對多年來考研數學真題各個章節考點的分布規律進行了細致的分析總結,現與大家分享,供各位考生參考,希望對大家有所幫助。下面對考研數學(三)中的中值定理及導數的應用和微分方程部分的真題考點進行分析總結。
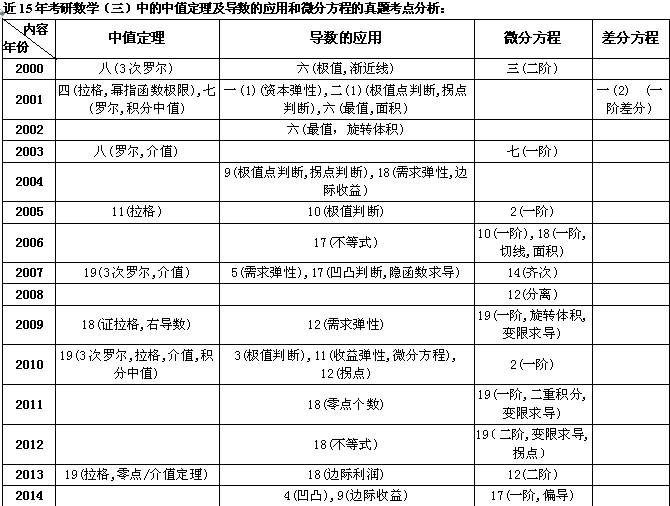
上面表格中數字表示相應年份的試卷中考題的題號,數字后面括號里的文字說明表示該考題涉及的主要考點或主要解題方法。
其中:1)“羅爾”指羅爾中值定理,“拉格”指拉格朗日中值定理,“柯西”指柯西中值定理,“泰勒”指泰勒公式,“洛必達”指洛必達法則;2)“一階”指一階線性微分方程,“二階”指二階常系數線性微分方程,“分離”指可分離變量的微分方程,“齊次”指齊次微分方程;3)“變限求導”指對變限積分函數求導;4)“不等式”指不等式證明;5)“零點”指函數的零點及零點定理;“介值”指連續函數的介值定理,6)“積分中值”指積分中值定理,7)“旋轉體積”指旋轉體的體積,8)“最值”指函數的最大值和最小值。
從近15年考題特點來看,在中值定理部分,出現頻率最高的是運用拉格朗日中值定理和羅爾中值定理的證明題,有時在一個題目中需要反復幾次連續運用羅爾或拉格朗日定理,這兩個定理在復習時一定要重點復習,熟練掌握,除此之外,對柯西中值定理和泰勒公式,大家也要有所了解并會簡單運用。中值定理的題型有一個顯著的特點,就是經常結合連續函數的介值定理、零點定理及積分中值定理進行綜合考查,因此,大家要學會對這些知識點的綜合運用,提高綜合解題能力。
在導數的應用部分,常考的題型包括:函數極值或最值的計算或判斷、曲線拐點和凹凸性的判斷、不等式的證明,有時會考函數的漸近線、函數的零點個數。除此之外,數學三的考題與數學一和數學二還有一個明顯不同的地方,那就是導數的經濟應用,包括:計算邊際成本、邊際利潤、需求彈性收益彈性等相關問題,大家應該掌握。
在微分方程部分,考題出現頻率很高,每年必考,而且考題有時不止一道,綜合性較強,如結合冪級數求和、求多元函數的二階偏導數等,各位考生對微分方程的各種題型和解題方法應該熟練掌握;微分方程這部分知識考得最多的題型是:一階線性微分方程和二階常系數線性微分方程,其中一階線性微分方程不僅是y對x的一階微分方程,還常出現x對y的一階微分方程,大家應靈活運用。除了一階和二階微分方程外,其它可能會出現的考點還包括:齊次微分方程、可分離變量的微分方程、一階和二階微分方程組。
上面就是對近15年考研數學(三)的中值定理、導數的應用和微分方程這幾部分內容的真題考點和題型特點所作的總結分析,供各位考生參考,以后蔡老師還會陸續對考研數學中其它考試內容的考點和題型特點及規律進行總結分析,希望各位考生留意查看,最后祝大家數學復習順利,考研馬到成功。




